Quaternary Signed Digit is a base-4 number system where a number is represented by one of the following 7 digits : -3,-2,-1,0,1,2,3. The advantage of this number system is that it allows carry free addition, thus speeding up the addition process.
Fast adders based on QSD are typical and there are several papers on this. In this post I have written the VHDL code for a 4 digit(each input being 12 bits) QSD adder. With a bit of editing, this code can be extended to handle larger input numbers.
One thing to be careful about is that while checking online for information on QSD adders, I came upon several papers with some little mistakes here and there. Even though these typos are small, but it can take hours of your debugging time, as it did in my case. So I recommend cross checking any circuit diagram you see online across several references.
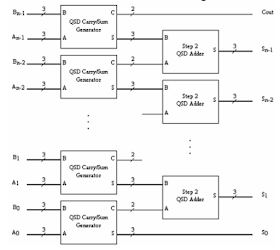
The Block diagram for the design is given below:
A QSD adder has two stages.
In the first stage we perform operation on a single digit from each operand to form an intermediate carry and sum. The carry is 2 bit and can have one of the three values from -1 to +1.
The sum is 3 bit and can have one of the 7 values from -3 to +3.
In the second stage, the intermediate carry and sum are simply added to form a single 3 bit sum which is between -3 to +3.
For an N digit QSD adder we have two input operands each N*3 bit in size. The Carry output is 2 bit in size and Sum output is N*3 bit in size.
For a N digit QSD adder we need N carry-sum generators and N-1 adders. How these blocks are connected together are shown in the block diagram above.
The boolean equations for these blocks are available in Page 4 of the second pdf shared in this blog. But some of these equations are not correct. But the circuit diagram given in the page 5 of the same pdf is correct and you can refer it to form the correct boolean equations.
The carry sum generator can be better understood by looking at the Table 2 and 3 of the first pdf. And table 5 gives more clarity on how the second step adder is working.
The VHDL codes are given below:
First step : Carry Sum Generator
--QSD carry sum generator.
library IEEE;
use IEEE.STD_LOGIC_1164.ALL;
use IEEE.NUMERIC_STD.ALL;
entity QSD_cs_gen is
Port ( A,B : in signed(2 downto 0);
S : out signed(2 downto 0);
C : out signed(1 downto 0)
);
end QSD_cs_gen;
architecture Behavioral of QSD_cs_gen is
begin
process(A,B)
variable anot,bnot : signed(2 downto 0);
variable ss : signed(2 downto 0);
variable cc : signed(1 downto 0);
variable temp1,temp2,temp3,temp4,temp5 : std_logic;
begin
anot := not A;
bnot := not B;
temp1 := not(A(1) or B(1));
temp2 := A(2) and bnot(0);
temp3 := B(2) and anot(0);
temp4 := temp1 and (temp2 or temp3);
cc(1) := (A(2) and B(2) and not(A(0) and B(0) and A(1) and B(1))) or temp4;
cc(0) := cc(1) or ((anot(2) and bnot(2)) and
((A(1) and B(1)) or (B(1) and B(0)) or (B(1) and A(0)) or (B(0) and A(1)) or (A(1) and A(0))));
ss(0) := A(0) xor B(0);
ss(1) := A(1) xor B(1) xor (A(0) and B(0));
temp1 := (ss(0) and (A(1) xor B(1)));
temp2 := (B(2) and anot(1) and bnot(0));
temp3 := (A(2) and bnot(1) and anot(0));
temp4 := ( A(0) and B(0) and anot(1) and bnot(1) and (A(2) or B(2)) );
temp5 := ( A(0) and B(0) and A(1) and B(1) and A(2) and B(2) );
ss(2) := temp1 or temp2 or temp3 or temp4 or temp5;
S <= ss;
C <= cc;
end process;
end Behavioral;
Second step : Addition of Intermediate Carry and Sum
--QSD step 2: adder for adding intermediate carry and sum.
library IEEE;
use IEEE.STD_LOGIC_1164.ALL;
use IEEE.NUMERIC_STD.ALL;
entity QSD_adder is
Port ( A : in signed(1 downto 0);
B : in signed(2 downto 0);
S : out signed(2 downto 0)
);
end QSD_adder;
architecture Behavioral of QSD_adder is
begin
process(A,B)
variable sum : signed(2 downto 0);
variable temp1,temp2,temp3,temp4 : std_logic;
begin
sum(0) := A(0) xor B(0);
sum(1) := A(1) xor B(1) xor (A(0) and B(0));
temp1 := A(1) and B(1);
temp2 := A(1) xor B(1);
temp3 := A(0) and B(0);
temp4 := temp1 or (temp2 and temp3);
sum(2) := A(1) xor B(2) xor temp4;
S <= sum;
end process;
end Behavioral;
4 Digit QSD Adder:
--4 digit QSD adder.
library IEEE;
use IEEE.STD_LOGIC_1164.ALL;
use IEEE.NUMERIC_STD.ALL;
entity QSDAdder is
Port ( A,B : in signed(11 downto 0);
Cout : out signed(1 downto 0);
S : out signed(11 downto 0)
);
end QSDAdder;
architecture Behavioral of QSDAdder is
component QSD_cs_gen is
Port ( A,B : in signed(2 downto 0);
S : out signed(2 downto 0);
C : out signed(1 downto 0)
);
end component;
component QSD_adder is
Port ( A : in signed(1 downto 0);
B : in signed(2 downto 0);
S : out signed(2 downto 0)
);
end component;
signal S0,S1,S2,S3 : signed(2 downto 0);
signal C0,C1,C2,C3 : signed(1 downto 0);
begin
--First stage to QSD addition : The 4 carry-sum generators.
carry_sum_gen1 : QSD_cs_gen port map (
A => A(2 downto 0),
B => B(2 downto 0),
S => S(2 downto 0),
C => C0
);
carry_sum_gen2 : QSD_cs_gen port map (
A => A(5 downto 3),
B => B(5 downto 3),
S => S1,
C => C1
);
carry_sum_gen3 : QSD_cs_gen port map (
A => A(8 downto 6),
B => B(8 downto 6),
S => S2,
C => C2
);
carry_sum_gen4 : QSD_cs_gen port map (
A => A(11 downto 9),
B => B(11 downto 9),
S => S3,
C => Cout
);
--Second stage to QSD addition : The addition of intermediate carry's and sum's
adder1 : QSD_adder port map (
A => C0,
B => S1,
S => S(5 downto 3)
);
adder2 : QSD_adder port map (
A => C1,
B => S2,
S => S(8 downto 6)
);
adder3 : QSD_adder port map (
A => C2,
B => S3,
S => S(11 downto 9)
);
end Behavioral;
Testbench for the 4 Digit QSD Adder:
--Testbench code which tests all combinations of inputs to a 4 digit QSD adder
library IEEE;
use IEEE.Std_logic_1164.all;
use IEEE.Numeric_Std.all;
entity QSDAdder_tb is
end;
architecture bench of QSDAdder_tb is
component QSDAdder
Port ( A,B : in signed(11 downto 0);
Cout : out signed(1 downto 0);
S : out signed(11 downto 0)
);
end component;
signal A,B: signed(11 downto 0);
signal Cout: signed(1 downto 0);
signal S: signed(11 downto 0) ;
--A function to convert any length QSD number to a signed integer.
function qsd2int ( A : SIGNED ) return signed is
variable res : signed(31 downto 0) := (others => '0');
variable num_digits : integer := (A'high+1)/3;
variable temp : signed(31 downto 0) := (others => '0');
variable ones : signed(31 downto 0) := (others => '1');
variable zeros : signed(31 downto 0) := (others => '0');
begin
for i in 0 to num_digits-1 loop
if(A(2+3*i) = '1') then --this part is just does sign extension
temp := ones(31 downto 3) & A(2+3*i downto 3*i);
else
temp := zeros(31 downto 3) & A(2+3*i downto 3*i);
end if;
res := res + shift_left(temp,2*i); --shift left and accumulate.
end loop;
return res;
end qsd2int;
signal A_dec,B_dec,S_dec,S_act : signed(31 downto 0) := (others => '0');
signal error : integer := 0;
begin
uut: QSDAdder port map ( A => A,
B => B,
Cout => Cout,
S => S );
--this is where we generate inputs to apply to the adder.
--4 digits for one number. and we have two numbers.
--so 8 for-loops to generate all combination of values for all digits.
stimulus: process
begin
wait for 5 ns;
for i in -3 to 3 loop
for j in -3 to 3 loop
for k in -3 to 3 loop
for l in -3 to 3 loop
A <= to_signed(i,3) & to_signed(j,3) & to_signed(k,3) & to_signed(l,3);
for m in -3 to 3 loop
for n in -3 to 3 loop
for o in -3 to 3 loop
for p in -3 to 3 loop
B <= to_signed(m,3) & to_signed(n,3) & to_signed(o,3) & to_signed(p,3);
wait for 10 ns;
end loop;
end loop;
end loop;
end loop;
end loop;
end loop;
end loop;
end loop;
wait;
end process;
--the outputs are checked here for error with actual sum.
check_results: process
variable A_dec1,B_dec1,S_dec1,S_act1 : signed(31 downto 0) := (others => '0');
begin
for i in 1 to 7**8 loop --7^8 total set of inputs.
wait for 10 ns;
A_dec1 := qsd2int(A);
B_dec1 := qsd2int(B);
--if carry out is -1 we subtract 256. or else we add if carry out is 1.
if(Cout = "11") then
S_dec1 := qsd2int(S)-256;
elsif(Cout = "01") then
S_dec1 := qsd2int(S)+256;
else --carry out is zero.
S_dec1 := qsd2int(S);
end if;
S_act1 := A_dec1+B_dec1;
--if result from adder and actual sum doesnt match increment "error"
if(S_dec1 /= S_act1) then
error <= error+1;
end if;
A_dec <= A_dec1;
B_dec <= B_dec1;
S_dec <= S_dec1;
S_act <= S_act1;
end loop;
wait;
end process;
end;
A bit of explanation on the VHDL codes:
The first two codes, QSD_cs_gen and QSD_adder, are simply based on the boolean equations and circuit diagram presented in the second pdf. Its a gate level code. Note that I have broken the long equations into several lines by using temporary variables. This adds clarity as well as makes the code you write less prone to error.
The third code, QSDAdder, is the 4 digit QSD adder, which connects the above two blocks in a structural level design.
The fourth code, QSDAdder_tb, is the testbench for testing the functionality of our adder. This is relatively complicated compared to the other three blocks of code.
Testbench has a function named qsd2int, which converts any QSD number into a signed number. Each digit of the QSD number is sign extended to 32 bits and then left shifted by a multiple of 2 before accumulatively adding to the result. Left shifting here simply means I am trying to multiply by 1,4,16,64 etc. based on the index of the digit.
In the testbench I want to test the design for all the possible combinations of inputs. There are two 4 digit QSD numbers and each number has 7 possible values. Which means that the number of sets of inputs is 7^(4+4) = 7^8 = 5764801. This is achieved in the process named stimulus.
The resultant sum from the Adder module are compared with the actual result in another process named check_results. If there is a mismatch in this comparison, a variable named error is incremented by 1. The Adder is fully working, if by the end of the simulation error is still 0.
VHDL codes and papers which I have referred to write the codes can be downloaded as a Zipped file from here.
Note that the Boolean equations in the second paper have some mistakes. But you can check the circuit diagram, which seems to be correct. Cross check with the VHDL codes if you are not sure.
The codes were simulated and tested successfully using Modelsim 10.4a.