VHDL: Synthesisable Code for Finding Square Root (With Testbench!)

            

UPDATE: A much more Synthesizable and Clocked Square Root Calculator is available here. 

    As you are probably aware, there is no built-in library function available in VHDL for finding the square root of an integer. There are several algorithms available for this, and in this article I have chosen to implement one of them using VHDL. 

    

    What I have used in this code is Non-Restoring Square Root algorithm. If you want to understand  the specifics of it, you can read it in this paper.

    I have used VHDL procedure to implement this algorithm. The whole function is combinatorial. So I have to warn you that its a bit of a resource eater, but you will get the result in just one clock cycle. The procedure is declared as follows:

procedure sqrt(variable d : in unsigned(31 downto 0); 

            variable root : out unsigned(15 downto 0); 

            variable remainder : out unsigned(15 downto 0)) is

The procedure takes one 32 bit unsigned integer and outputs a 16 bit square root and a 16 bit remainder. What I meant by remainder here is simply the difference between the input integer and square of the output square root. 

So 

Remainder = d - root*root;

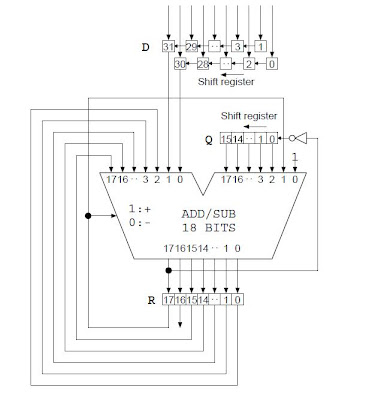
The block diagram of the algorithm is given below(taken from this paper):

      Here, D is the unsigned input number. R is the remainder of the operation for non-perfect squares. Q contains the square root of D.

I have written the VHDL procedure and directly used it within a self checking testbench. The testbench can be used to easily verify the working of any number of inputs without you needing to do any manual verification. Thats why its called a self checking testbench.

Square Root procedure with Testbench:

--library declarations
library ieee;
use ieee.std_logic_1164.all;
use ieee.numeric_std.all;
--we need this library to use random number generator function.
use ieee.math_real.all;
 
--entity for testbenches are always empty
entity tb_square_root is
end tb_square_root;
 
architecture behavior of tb_square_root is 
 
--procedure for finding the square root of a 32 bit unsigned number.
--'d' is the input number, 'root' is the square root, 
--'remainder' is 'd minus square_of_squareRoot'.
 procedure sqrt(variable d : in unsigned(31 downto 0); 
        variable root : out unsigned(15 downto 0); 
        variable remainder : out unsigned(15 downto 0)) is
    variable a : unsigned(31 downto 0):=d;  --original input.
    variable q : unsigned(15 downto 0):=(others => '0');  --result.
    --'left' and 'right' are inputs to adder/sub. 'r' is remainder.
    variable left,right,r : unsigned(17 downto 0):=(others => '0');  
    variable i : integer:=0;  --loop index
begin
    for i in 0 to 15 loop  --iterate 16 times.
        right := q & r(17) & '1';  --'&' is used for concatenation in VHDL
        left := r(15 downto 0) & a(31 downto 30);
        a := a(29 downto 0) & "00";  --shifting left by 2 bit.
        if ( r(17) = '1') then
            r := left + right; --add
        else
            r := left - right; --subtract
        end if;
        q := q(14 downto 0) & not r(17);  --left shift and pad msb of 'r'
    end loop;
    root := q;  --assign output
    a := d-q*q;  --calculate remainder manually
    remainder := a(15 downto 0);  --take only lsb 16 bits for output.
end procedure;  --END of procedure
    
--internal signals used in the testbench. 
--They are used for checking the inputs and outputs in simulation waveform.
signal square : unsigned(31 downto 0);  
signal root : unsigned(15 downto 0);
signal remainder : unsigned(15 downto 0);

begin
 
-- Stimulus process
stim_proc: process
    variable seed1, seed2 : integer := 1;
    variable rand : real;
    variable int_rand : integer;
    variable a : unsigned(31 downto 0);  --original input.
    variable rooot : unsigned(15 downto 0):=(others => '0');  --result.
    variable r : unsigned(15 downto 0):=(others => '0');  --result.
begin
    --you can iterate as many times as you want. In each iteration different random numbers 
    --will be used for testing. The results are automatically checked for their correctness.
    --So we call this a 'self checking testbench'.
    for i in 0 to 1000 loop  
        --generate a random number for a.
        --Value of 'rand' is between 0 and 1. 
        --Multiply 'rand' by 2^N and then round down to get an integer.
        uniform(seed1, seed2, rand);  
        int_rand := integer(trunc(rand*real(2**30))); 
        a := to_unsigned(int_rand,32);
        --call the 'sqrt' procedure. All inputs and outputs are variables here.
        sqrt(a,rooot,r);
        --check if the result is correct.
        --two conditions are checked to make sure that the result is correct. 
        --1st we check that the input is greater than or equal to square of 'output square root'.
        assert (a >= rooot*rooot and a < (rooot+1)*(rooot+1))report "ERROR:incorrect square root";
        --2nd we check that square of 'output square root' when added to 'remainder' is equal to input number.
        assert a = rooot*rooot+r report "ERROR:incorrect remainder";
        --assign the operands and results to signals so that we can see it in the simulation waveform.
        square <= a;
        root <= rooot;
        remainder <= r;
        --wait a bit before trying a new set of inputs. 
        --Otherwise we wont be able to see the different iterations in the simulation waveform.
        wait for 10 ns;
    end loop; 
    wait;  --wait endlessly. We are done with testing!
end process;

end;

The code is well commented, so you probabaly wont need me to explain any further. The code was simulated using modelsim. Let me share some screenshots of the simulation waveform below:

Simulation waveform from Modelsim:

Note :- The sqrt procedure was successfully synthesised using Xilinx Vivado 2023.2.